题意
给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。
难度
困难
标签
排序、链表、堆
示例
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
分析
合并 K 个升序链表，很容易就让我们想到之前做过的 021.合并两个有序链表，这道题是升级版，合并 K 个。
021 题解的思路是通过比较两个链表的头节点，更小的那个就是新链表的头节点，再从剩余的里面找到下一个节点。
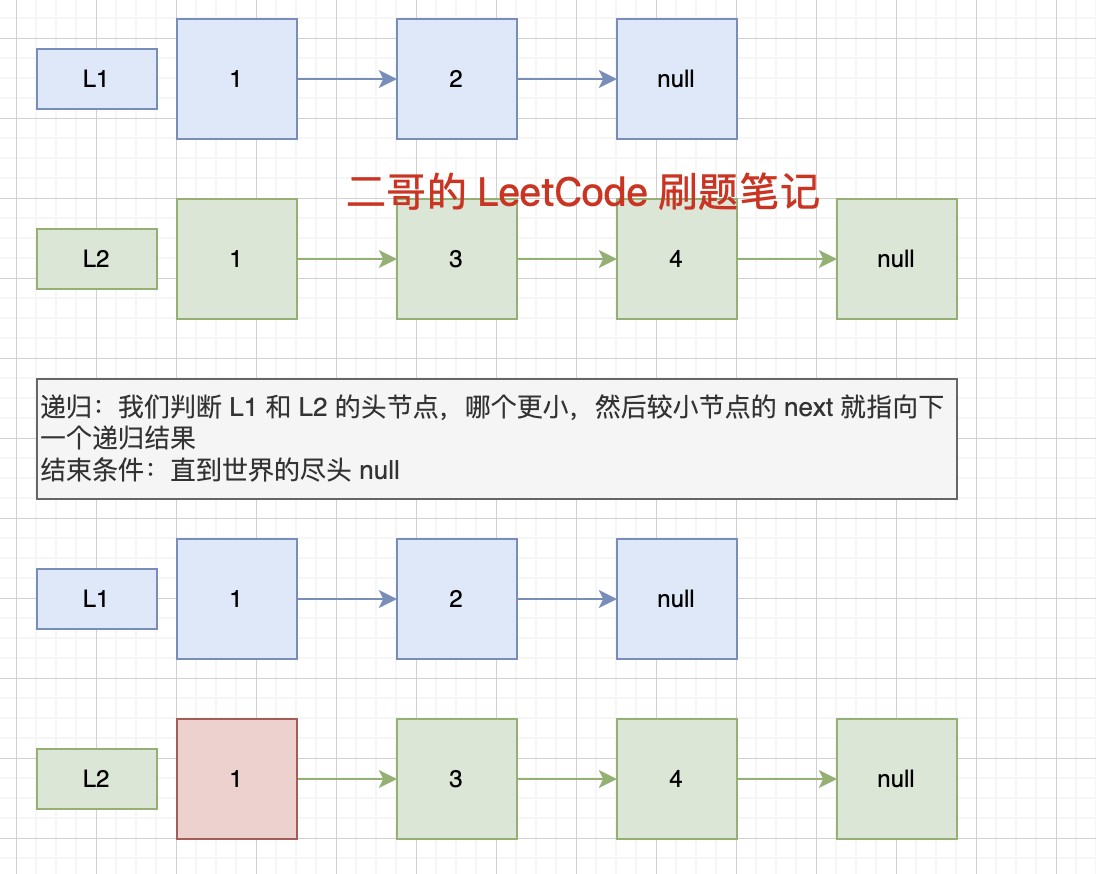
那我们能不能用相同的方法来完成 K 个升序链表的合并呢？
第一个链表与第二个链表合并，然后新的链表再与第三个链表合并……，以此类推，看上去能实现我们的目的。
但很遗憾，这样做的话，每一次合并后的新链表就会非常臃肿，并且在与第 K 个链表合并时，之前链表的节点会多次被访问。
第一个链表被访问k - 1次，第二个链表被访问k - 2次……
看来不太行啊，我们需要另寻他路。
堆。
堆。
堆。
好了，我来告诉大家答案啦，我们可以把 k 个链表的节点都扔到堆中，然后就可以快速得到最小的那个节点。堆顶的那个节点就是最小的。
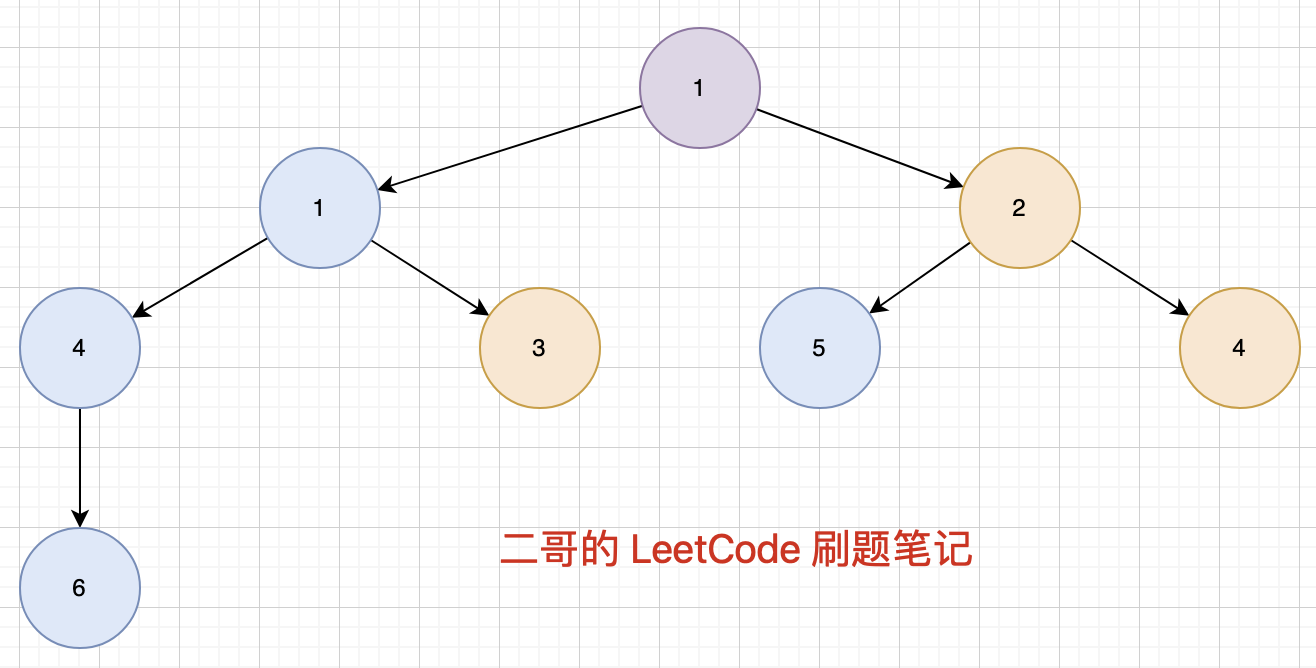
每次把堆顶的那个节点取出来放到新的链表里，是不是瞬间一道难题就变成了一道简单题呢？
先不着急看题解，我们来讲讲最小堆。
上图中的堆就叫最小堆，Min Heap，一种特殊的完全二叉树，满足以下性质：对于树中的每个非叶子节点，节点的值都小于或等于其子节点的值。
这个特质确保了树的根节点总是所有节点中的最小值。
最小堆支持高效的数据插入和删除最小元素的操作，这使得它非常适合用来实现优先级队列（Priority Queue）。
优先级队列允许按照一定的优先级顺序（如从小到大或从大到小）移除和添加数据。
- 插入操作：当插入一个新元素时，元素会被放在树的底部，然后，这个元素会和它的父节点比较，如果新元素小于父节点，它们会交换位置。这个过程会一直持续，直到新元素的父节点小于或等于新元素，或者新元素到达了根节点。
- 删除操作：删除最小元素通常意味着删除根节点。删除根节点后，通常会将最后一个元素移动到根节点的位置，然后进行下沉操作（与子节点比较并与较小的子节点交换），直到恢复最小堆的性质。
来具体模拟一下哈。
初始最小堆
假设我们有一个初始的最小堆，如下所示：
5
/ \
7 9
/ \
10 15
插入新元素
现在，我们尝试插入一个新元素 6 到这个最小堆中。
①插入：首先，我们将 6 放在树的底部，以保持完全二叉树的结构。完全二叉树要求除了最后一层外，每一层都被完全填满，当插入一个新元素时，它总是被添加到这个完全二叉树的最后一个位置，以保持树的完整性和平衡。
5
/ \
7 9
/ \ \
10 15 6
②、调整：由于 6 小于其父节点 9，我们需要调整堆，以恢复最小堆的性质。6 和 9 交换位置。
5
/ \
7 6
/ \ \
10 15 9
现在，最小堆的性质恢复了，插入操作完成。
删除最小元素
接下来，我们尝试删除最小元素，即当前堆顶的 5。
①、删除：移除根节点 5，通常我们会将最后一个元素（这里是 9）移动到根节点的位置。
9
/ \
7 6
/ \
10 15
②、调整：由于 9 大于其子节点 6 和 7，我们需要调整堆。9 应该与其最小的子节点 6 交换位置，以恢复最小堆的性质。
6
/ \
7 9
/ \
10 15
现在，最小堆的性质再次恢复了，删除操作完成。
可以看到，刚好与我们的需求相符，我们可以通过最小堆来实现合并 K 个升序链表。
在 Java 中，优先级队列 PriorityQueue 就可以用来实现一个最小堆，我们通过重写 Comparator 接口中的 compare() 方法，定义出优先顺序，让 PriorityQueue 按照节点（ListNode）的值（val）大小排序即可。
OK，我们先来看比较规则：
static Comparator<ListNode> cmp = new Comparat
1人已点赞
回复