032.最长有效括号

鲁迅说过，项目告一个段落后，我们就可以重启二哥的 LeetCode 刷题笔记了，希望大家能够坚持下去，一起进步。

题意

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

难度

困难

示例

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

分析

还记得有效括号那道题吗？

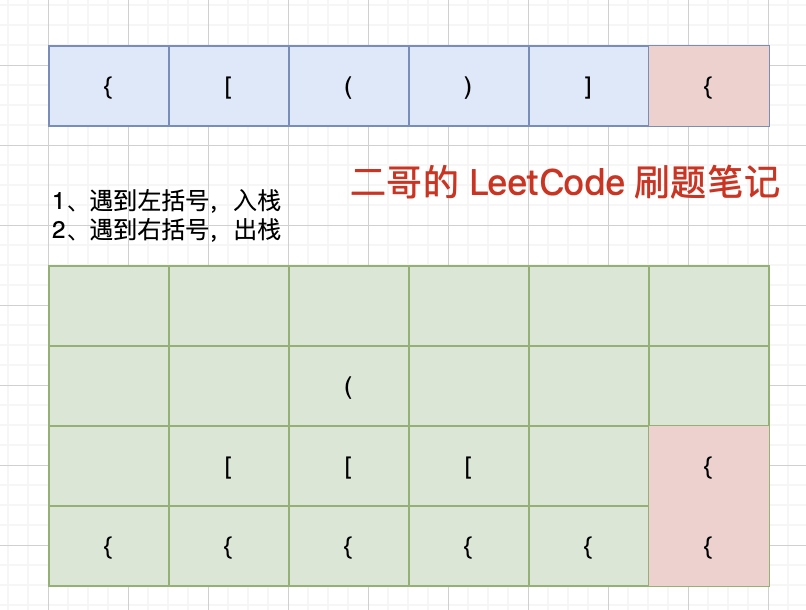
当时，我们利用了栈这个数据结构，当遇到一个右括号，就看一看栈内有没有与之匹配的左括号，如果栈为空或者说栈顶的左括号与之不匹配（除了小括号()还有中括号[]和大括号{}），那么它就不是一个有效的括号序列。

那这道题我们同样可以使用栈这个数据结构来解决。先来回顾一下栈的基本操作：

stack.push(-1); // 入栈
stack.pop(); // 出栈
stack.peek(); // 查看栈顶元素

接下来，我们需要搞清楚最长有效括号子串的特点：

• 每一个左括号 '(' 都有一个对应的右括号 ')'。
• 括号之间的嵌套关系是正确的，比如说 (()())、((()))、()()()。

然后，我们需要解决如何得出最长有效括号子串的长度。

新建一个栈，用来存放括号的下标。由于下标是从 0 开始的，我们可以在栈中放入一个 -1，表示栈底，这样更方便计算边界条件。

比如说对于 ()，初始状态是 [-1]，遇到左括号 (，我们将它的下标压入栈中，此时栈内是 [-1,0]。

遇到右括号 )，我们将栈顶的元素弹出，此时栈内是 [-...