鲁迅曾说过，有一段时间没有刷二哥的 LeetCode 刷题笔记了，心里痒痒的，今天我们开始刷 N 皇后吧，这道题可有意思了，比天天背八股来得开心多了。

题意

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

难度

困难

示例

示例 1：

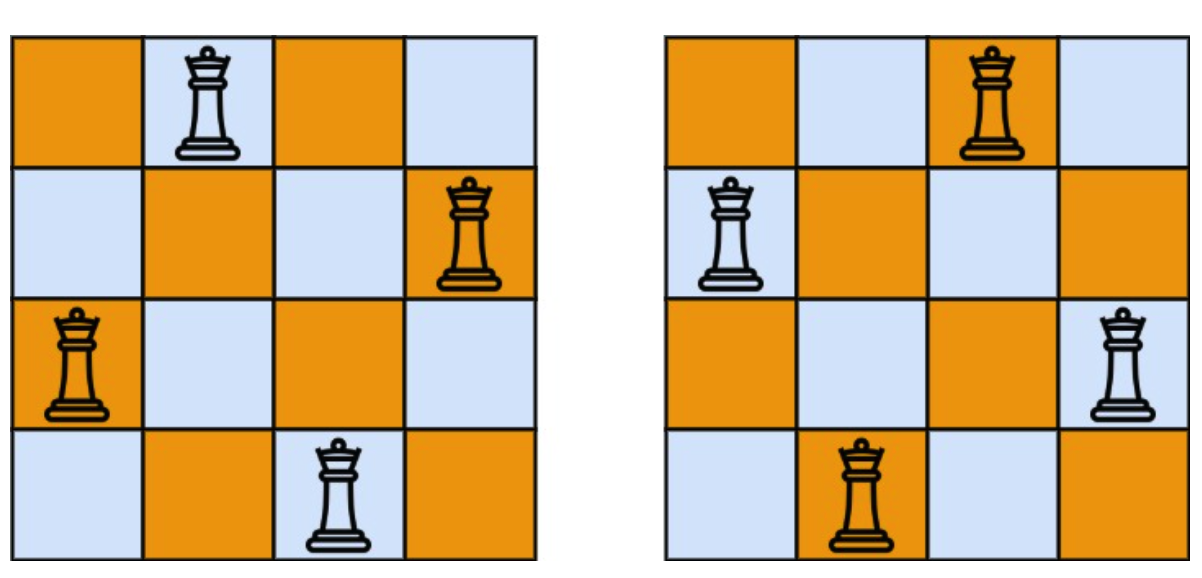
输入：n = 4

输出：[
[".Q..",
 "...Q",
 "Q...",
 "..Q."],
["..Q.",
 "Q...",
 "...Q",
 ".Q.."]]

解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

分析

N 皇后是一道非常经典的递归+回溯题目，但是这并不意味着它就非常的难，相反，合理运用递归+回溯的知识，我们其实可以“不费吹灰之力”就解出这道题目（信心一定要足😄）。

我们知道，一个 皇后 能够攻击她所在的 行、列、斜线上的棋子，那我们就直接从第一行开始，逐行放置皇后，然后判断当前位置是否合法，如果合法，我们就继续放置下一个皇后，如果不合法，我们就回溯到上一步，重新放置皇后。

非常暴力，但很容易上手。

class Solution {
    // 解决 N 皇后问题
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> solutions = new ArrayList<>();
        // 初始化棋盘
        char[][] board = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                board[i][j] = '.';
            }
        }
        // 开始递归查找所有解
        backtrack(solutions, board, 0, n);
        return solutions;
    }

    // 回溯方法
    private void backtrack(List<List<String>> solutions, char[][] board, int row, int n) {
        // 如果已成功放置完所有皇后，将当前棋盘方案加入 solutions
        if (row == n) {
            solutions.add(construct(board));
            return;
        }

        // 尝试在当前行的每一列放置皇后
        for (int col = 0; col < n; col++) {
            // 检查当前位置是否安全
            if (isValid(board, row, col, n)) {
                // 放置皇后
                board[row][col] = 'Q';
                // 递归处理下一行
                backtrack(solutions, board, row + 1, n);
                // 回溯，撤销当前放置
                board[row][col] = '.';
            }
        }
    }

    // 检查在 (row, col) 位置放置皇后是否安全
    private boolean isValid(char[][] board, int row, int col, int n) {
        // 检查列上是否有皇后
        for (int i = 0; i < row; i++) {
            if (board[i][co