鲁迅曾说过，有过 N 皇后的经验后，这道题就是纯粹的送分题了，因为题目的核心解法是完全一样的，只不过这道题目只需要返回方案的个数而已。上一道题要求返回的是具体的方案，换句话说，只需要在上一道题目的基础上稍作修改即可。

题意

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

可以参考上一题：051.N 皇后

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

难度

困难

示例

示例 1：

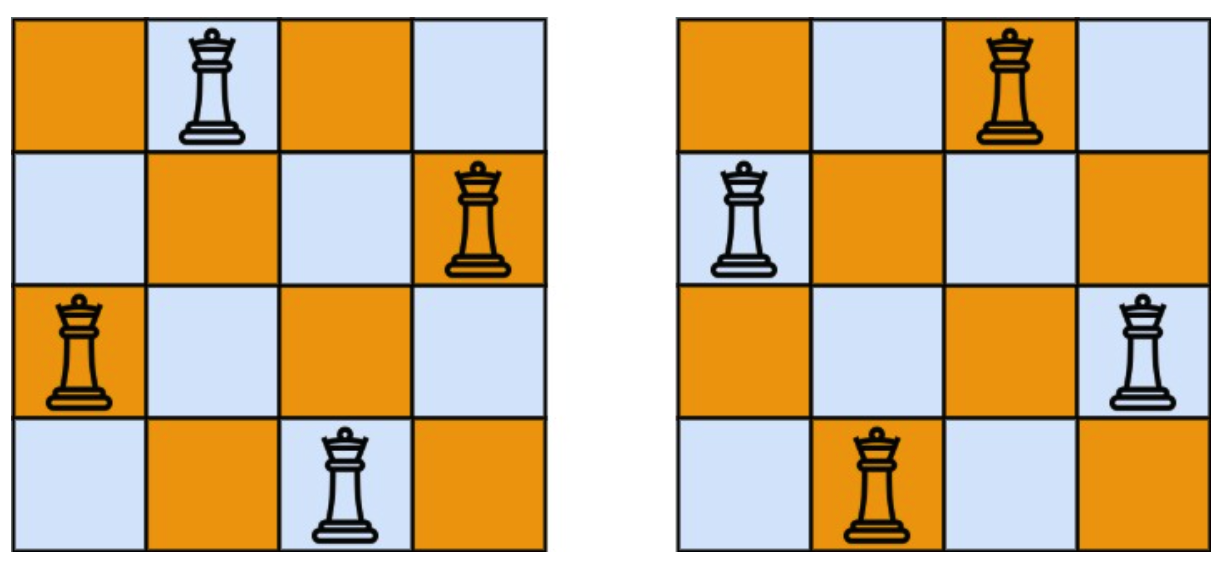
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

分析 1

在051.N皇后 中，我们已经将递归+回溯讲得很清楚了，如果理解了 051. N 皇后，这道题目只能算是一个弱化版本，因为我们已经把方案求解出来了，这道题只需要返回方案的个数即可。

只需要简单改几个地方，先来看题解。

class Solution {
    // 记录解的数量
    int solutions = 0;
    // 解决 N 皇后问题
    public int totalNQueens(int n) {
        // 初始化棋盘
        char[][] board = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                board[i][j] = '.';
            }
        }
        // 开始递归查找所有解
        backtrack(board, 0, n);
        return solutions;
    }

    // 回溯方法
    private void backtrack(char[][] board, int row, int n) {
        // 如果已成功放置完所有皇后，将当前棋盘方案加入 solutions
        if (row == n) {
            solutions = solutions + 1;
            return;
        }

        // 尝试在当前行的每一列放置皇后
        for (int col = 0; col < n; col++) {
            // 检查当前位置是否安全
            if (isValid(board, row, col, n)) {
                // 放置皇后
                board[row][col] = 'Q';
                // 递归处理下一行
                backtrack(board, row + 1, n);
                // 回溯，撤销当前放置
                board[row][col] = '.';
            }
        }
    }

    // 检查在 (row, col) 位置放置皇后是否安全
    private boolean isValid(char[][] board, int row, int col, int n) {
        // 检查列上是否有皇后
        for (int i = 0; i < row; i++) {
            if (board[i][col] == 'Q') {
                return false;
            }
        }

        // 检查左上方对角线上是否有皇后
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[